This last week I was downed by illness. During the day when I had the highest fever I took a rapid SARS-COV-2 self-test. It came out positive. Even though I got covid over two years ago and have taken three vaccines over the past year and a half it seemed it was time again. Since I recently had a course in statistics and probability I found it fun to try my new skills with the information provided by the self-test. The documentation compared the results from the test with PT-PCR Results. 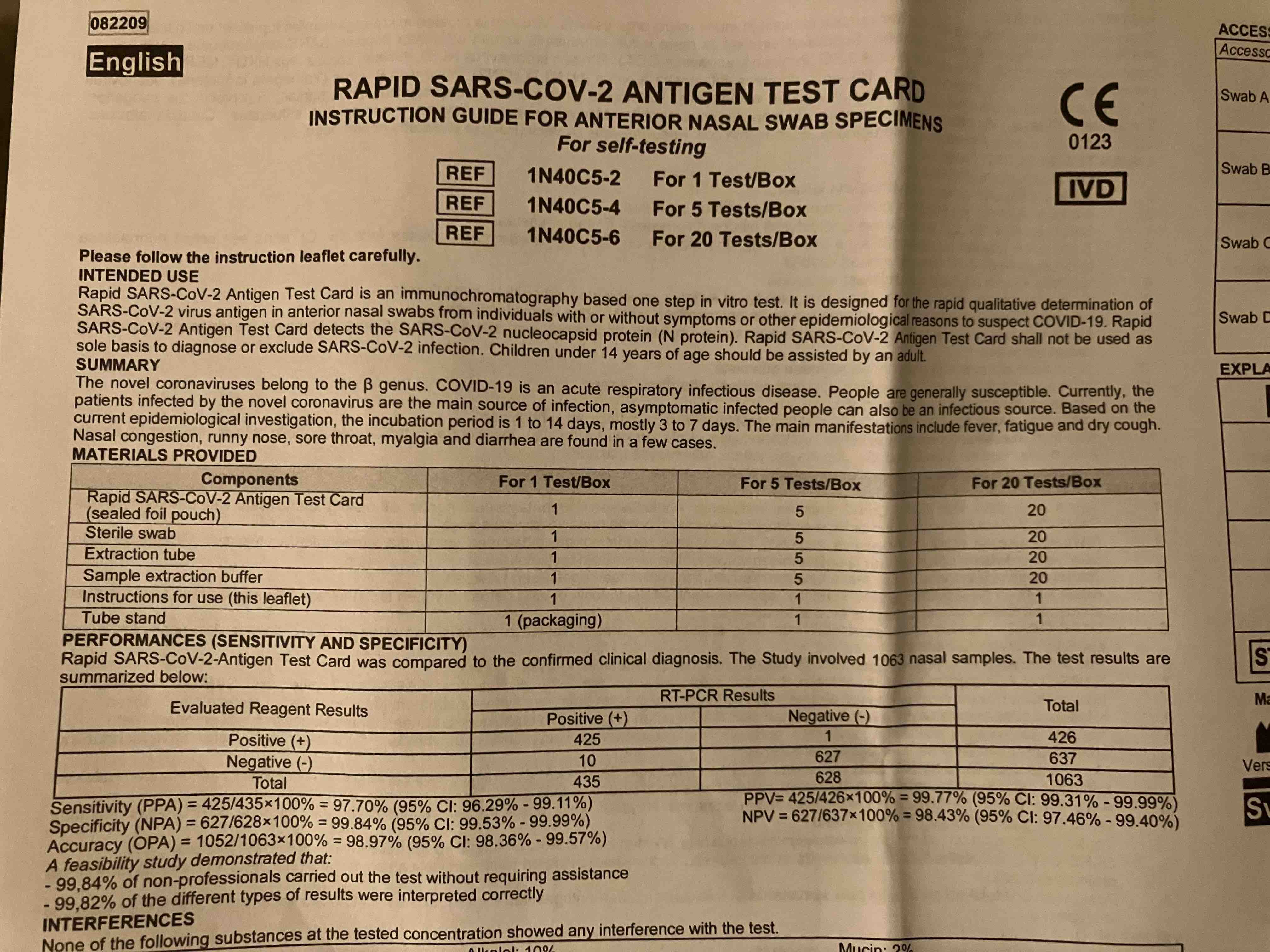Covid self-test

I want to know an approximate probability that I actually had a covid infection. Lets say that A is the is the stochastic variable that tells if the self-test is positive. B is the stochastic variable that tells if the PT-PCR is positive. Since my test said that A is positive, then what is the probability that I have an infection - that the PT-PCR also is positive?

With help from Bayes Theorem we get the following equation:

$$ P(B|A) = {P(A|B)P(B) \over P(A|B)P(B) + P(A|B^*)P(B^*)} $$

And we set up the following models:

$$ P(A|B) = p \textrm{ and } P(A|B^*) = q $$

To approximate p and q we simple use the lab results displayed on the documentation. We use a binominal distribution from the positive and negative results from the PT-PCR; Bin(435,p) and Bin(628,q).

$$ p^{*}_{obs} = {425 \over 435} \approx 0.977 \textrm{ and } q^{*}_{obs} = {1 \over 628} \approx 0.002 $$

Lastly, I will make a guess that 1% of the population has the infection. I could not find any source for a recent approximation but it is not to much of a wild guess. We can now go back and utilize Bayes theorem:

$$ P(B|A) = {0.977*0.01 \over 0.977*0.01 + 0.002*0.99 } \approx 0.83$$

The conclusion is that there is a 83% risk that I actually got an infection. Notes: If the amount of infection in the population is greater than 1% - the risk would be even higher. At 2% the risk will be about 90%. This makes sense, both by reasoning and by looking at the math.